尽量说人话

二叉树

模板

递归

traverse(root) {
    // 前序遍历
    traverse(root.left)
    // 中序遍历
    traverse(root.right)
    // 后序遍历
}

迭代

const res = []
const stack = []
root && stack.push(root)
while (stack.length) {
  const node = stack.pop()
  if (node == null) {
    res.push(stack.pop().val)
    continue
  }
  if (node.right) stack.push(node.right) // 右
  if (node.left) stack.push(node.left) // 左
  stack.push(node) // 中
  stack.push(null)
}
return res

102. 二叉树的层序遍历

层序遍历的关键是用一个数组保存上一层的节点，需要注意在遍历这个保存节点的数组时，注意缓存长度，因为遍历过程中数组长度会变化（js 中普通 for 循环数组长度变化会影响遍历范围）

var levelOrder = function (root) {
  const res = []
  if (root == null) {
    return res
  }
  const q = [root]
  while (q.length) {
    const len = q.length // 注意缓存长度，因为遍历过程中数组长度会变化
    const path = []
    for (let i = 0; i < len; i++) {
      const node = q.shift()
      path.push(node.val)
      if (node.left) q.push(node.left)
      if (node.right) q.push(node.right)
    }
    res.push(path)
  }
  return res
}

104. 二叉树的最大深度

递归

先确定好函数的返回值，树的深度。

终止条件是什么？root == null时，返回深度为 0

递推条件：左右子树深度的最大值加上 1

var maxDepth = function (root) {
  if (root == null) return 0
  return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1
}

112. 路径总和

递归

递归的基本思想，确定好函数要返回什么，然后从结束条件开始思考

这里我们需要返回的是是否有一条路径的值加起来等于 targetSum

结束条件是：

1. root 为 null，返回 false

2. 到叶子节点了，返回 targetSum === root.val

然后思考递推关系，去掉一个节点之后，左右子树只要有一条可以走通就行，那么用||，并且 targetSum 需要减去root.val

var hasPathSum = function (root, targetSum) {
  if (root === null) {
    return false
  }

  if (root.left === null && root.right === null) {
    return targetSum === root.val
  }
  return hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.right, targetSum - root.val)
}

129. 求根节点到叶节点数字之和

DFS

用 preSum 记录之前的总和，记得到叶子节点（root.left == null && root.right == null）的时候就应该返回sum，不然结果会变成 2 倍

const dfs = (root, prevSum) => {
  if (root === null) {
    return 0
  }
  const sum = prevSum * 10 + root.val
  if (root.left == null && root.right == null) {
    return sum
  } else {
    return dfs(root.left, sum) + dfs(root.right, sum)
  }
}

var sumNumbers = function (root) {
  return dfs(root, 0)
}

105. 从前序与中序遍历序列构造二叉树

我们需要首先找到root在中序数组中的位置，来分割左子树和右子树

而前序数组的第一个值就是root，所以遍历中序数组找到root即可（这里可以用 map 保存中序数组中每个值的位置来优化）

然后我们就需要根据中序数组root的位置来分割左子树和右子树

var buildTree = function (preorder, inorder) {
  // slice 切分数组 速度较慢
  // if (preorder.length === 0) return null
  // const rootValue = preorder[0]
  // const index = inorder.indexOf(rootValue)
  // const left = buildTree(preorder.slice(1, index + 1), inorder.slice(0, index))
  // const right = buildTree(preorder.slice(index + 1), inorder.slice(index + 1))
  // const root = new TreeNode(rootValue, left, right)

  const hash = new Map()
  for (let i = 0; i < inorder.length; i++) {
    hash.set(inorder[i], i)
  }

  return build(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1, hash)
}

function build(preorder, p_start, p_end, inorder, i_start, i_end, hash) {
  if (p_start > p_end) {
    return null
  }
  const rootVal = preorder[p_start]
  const index = hash.get(rootVal)

  const leftChild = index - i_start

  const root = new TreeNode(rootVal)

  root.left = build(preorder, p_start + 1, p_start + leftChild, inorder, i_start, index - 1, hash)

  root.right = build(preorder, p_start + leftChild + 1, p_end, inorder, index + 1, i_end, hash)

  return root
}

199. 二叉树的右视图

DFS

var rightSideView = function (root) {
  const res = []
  dfs(root, res, 0)
  return res
}

function dfs(root, res, depth) {
  if (root == null) {
    return
  }

  if (depth == res.length) {
    // 如果当前节点所在深度还没有出现在res里，说明在该深度下当前节点是第一个被访问的节点，因此将当前节点加入res中。
    res.push(root.val)
  }

  depth++
  dfs(root.right, res, depth)
  dfs(root.left, res, depth)
}

BFS

var rightSideView = function (root) {
  if (root == null) return []
  let path = [root]
  const res = []

  while (path.length) {
    const len = path.length
    for (let i = 0; i < len; i++) {
      const node = path.shift()
      if (node.left) path.push(node.left)
      if (node.right) path.push(node.right)
      if (i === len - 1) res.push(node.val)
    }
  }
  return res
}

链表

141. 环形链表

快慢指针

我们设置两个指针分别从head出发，每次走一步；另一个从head.next出发，每次走两步，如果最后相交（相等），就说明链表有环

注意循环的条件是p2 && p2.next

var hasCycle = function (head) {
  if (!head || !head.next) {
    return false
  }

  let p1 = head
  let p2 = head.next

  while (p2 && p2.next) {
    if (p1 === p2) {
      return true
    }
    p1 = p1.next
    p2 = p2.next.next
  }

  return false
}

206. 反转链表

递归

使用递归，我们需要先明确三点：递归函数的输出、输出和递归函数的终止条件

把整个函数当做一个递归函数来看

首先是第一点，我们输入的是头结点 head

那么第二点，输出就是反转之后的链表的头节点，就叫last好了

最后是第三点，什么时候/条件结束？这个一下子想不出来也没关系，我们先来想想递归的过程应该是怎么样的？

开始递归

const last = reverseList(head.next)

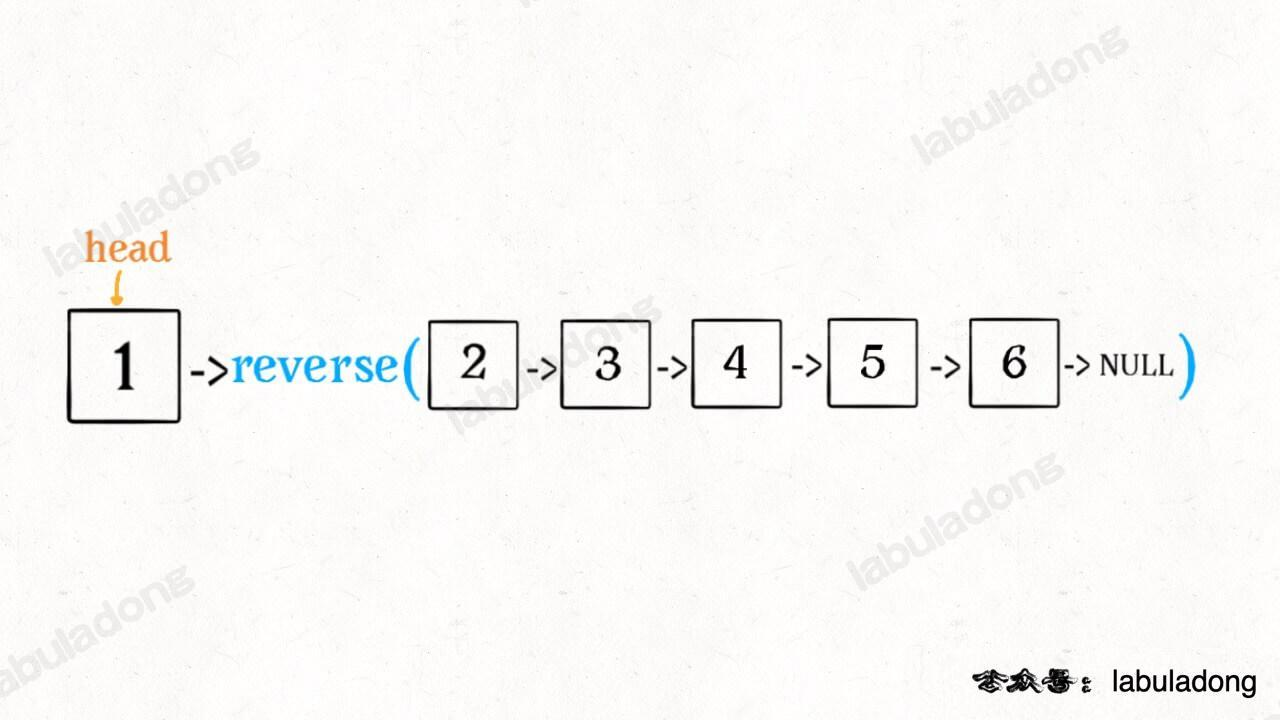
我们会得到这样的状态：

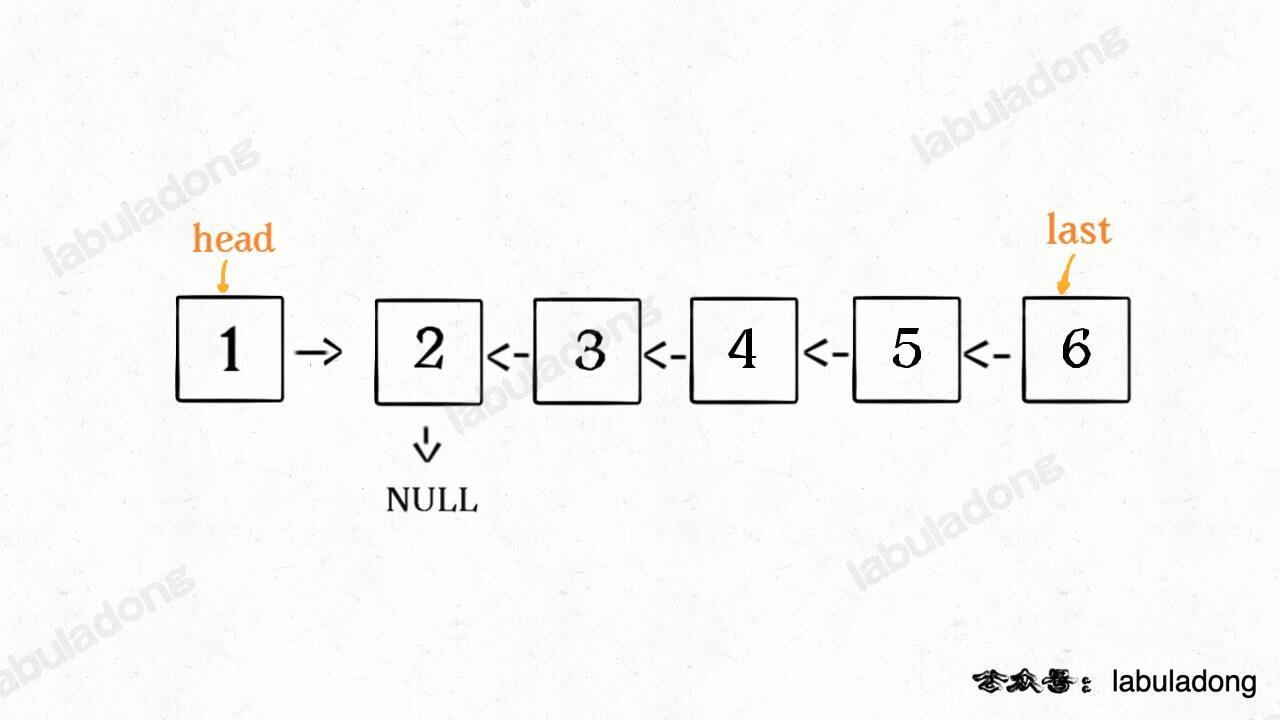
现在就只有 head 节点的指向不对了，head 应该指向 null，而2应该指向1

所以我们需要

head.next.next = head.next // 将 2 指向 head
head.next = null // 将 head 指向 null

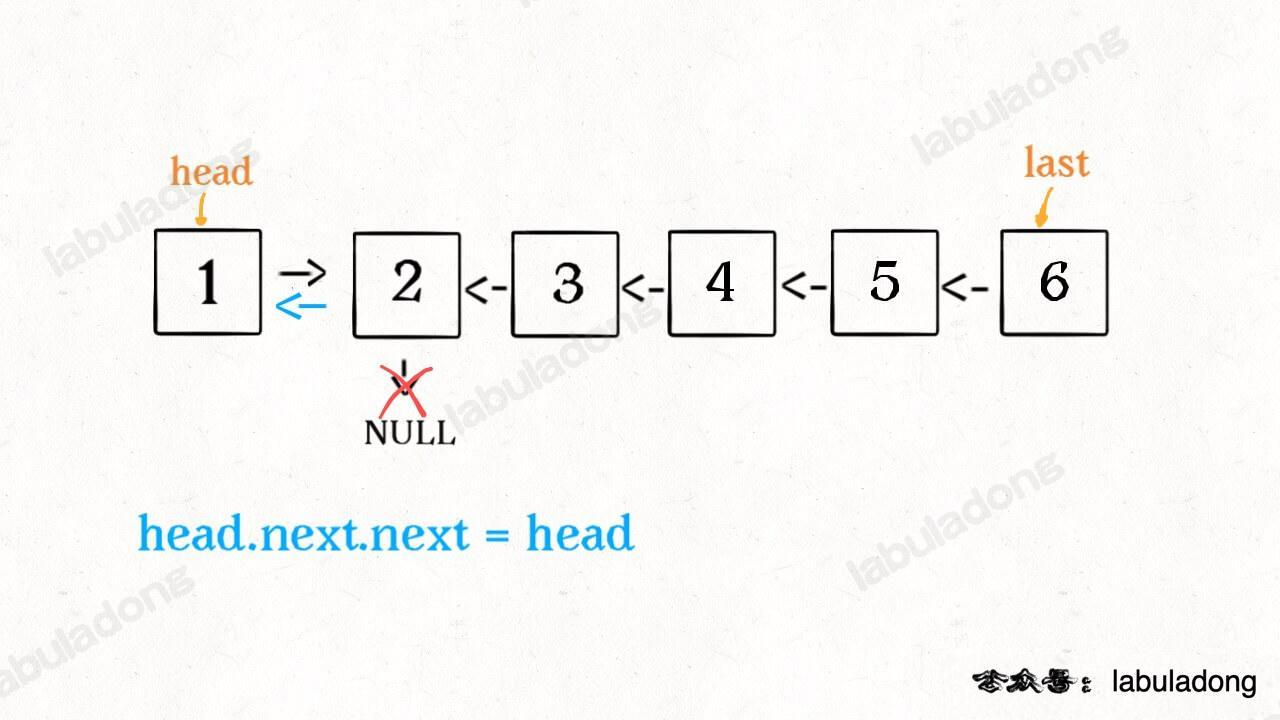
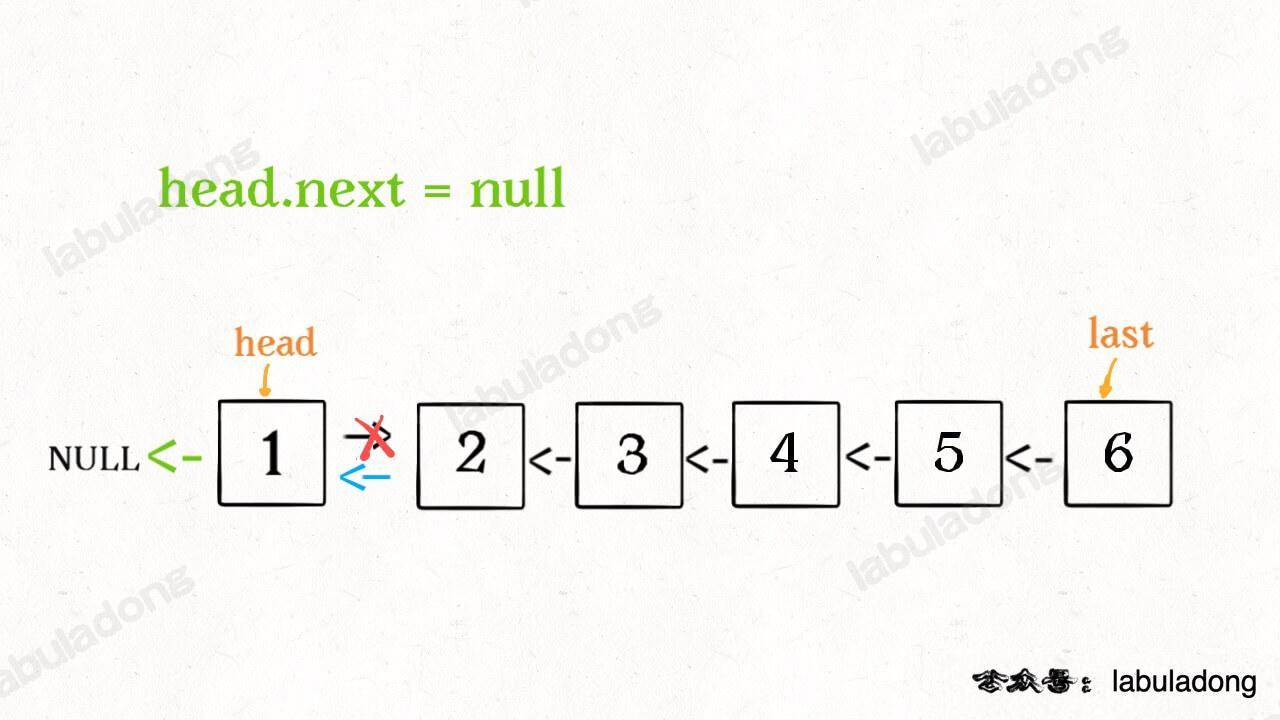
链表成功反转

清楚了递归过程之后，终止条件也很容易想到了，就是head.next == null的情况，即到了最后一个节点，直接返回该节点即可

var reverseList = function (head) {
  // head == null 处理输入数据为 null 的情况
  // head.next == null 是递归终止条件
  if (head == null || head.next == null) {
    return head
  }
  const last = reverseList(head.next)
  head.next.next = head
  head.next = null
  return last
}

迭代

我们的目的是不断地让当前节点指向前一个节点（头结点指向null）

初始状态

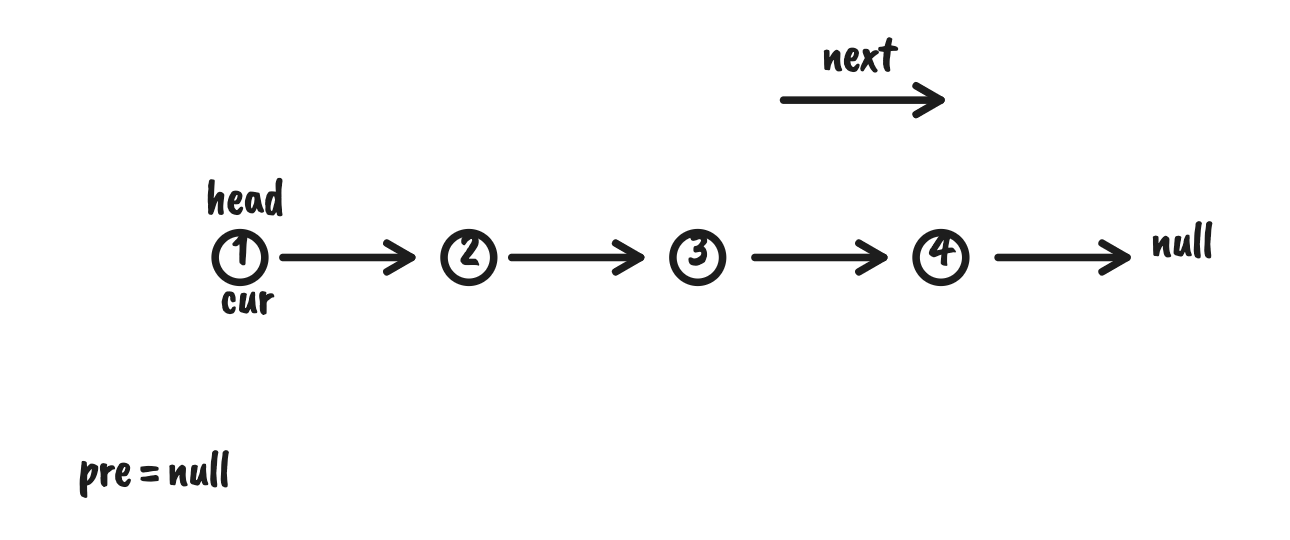
迭代过程

cur 指向 pre 后，pre 和 cur 的位置不断前移，最后返回观察图，应该返回 pre

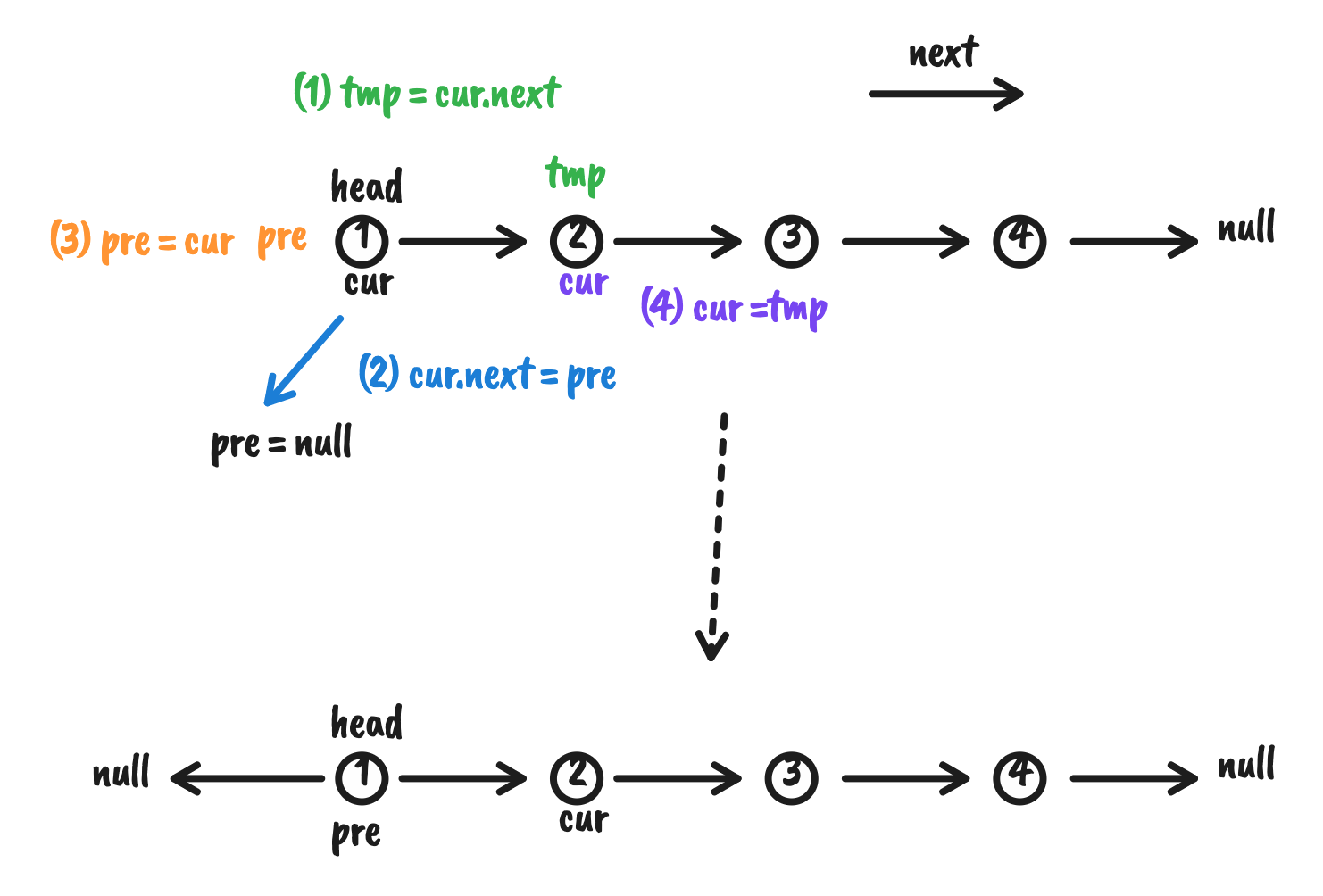
var reverseList = function (head) {
  let pre = null
  let cur = head
  while (cur) {
    const tmp = cur.next
    // 当前节点指向前一个节点
    cur.next = pre
    // 位置前移
    pre = cur
    cur = tmp
  }
  return pre
}

剑指 Offer 22. 链表中倒数第 k 个节点

用两个指针，它们之间相隔k个距离，那么当前面的指针到达末尾，后面的指针就正好指向倒数第 k 个节点

var getKthFromEnd = function (head, k) {
  let p1 = head
  let p2 = head
  while (k && p2) {
    p2 = p2.next
    k--
  }

  while (p2) {
    p1 = p1.next
    p2 = p2.next
  }

  return p1
}

21. 合并两个有序链表

var mergeTwoLists = function (list1, list2) {
  let p1 = list1
  let p2 = list2
  const head = new ListNode()
  let p = head

  while (p1 && p2) {
    if (p1.val <= p2.val) {
      p.next = p1
      p1 = p1.next
    } else {
      p.next = p2
      p2 = p2.next
    }
    p = p.next
  }

  p.next = p1 ? p1 : p2

  return head.next
}

160. 相交链表

思路就是：我吹过你吹过的晚风

设置两个指针，分别指向两个链表的头节点，同时移动，到末尾之后就重新指向另一个链表的头节点，直到两个指针指向的节点相等（包括同时为null）

var getIntersectionNode = function (headA, headB) {
  if (headA === null || headB === null) return null
  let p1 = headA,
    p2 = headB
  while (p1 !== p2) {
    p1 = p1 === null ? headB : p1.next
    p2 = p2 === null ? headA : p2.next
  }
  return p1
}

字符串

5. 最长回文子串

双指针

两个指针从中心开始扩散寻找回文串，因为需要考虑回文串长度的奇偶情况，所以需要两个指针，代表回文串的中心

注意palindrome函数返回回文串时，l 和 r 已经越界了，需要向前收缩一步返回，即s.substring(l + 1, r)

var longestPalindrome = function (s) {
  let res = ''
  for (let i = 0; i < s.length; i++) {
    const s1 = palindrome(s, i, i) // 回文串长度为奇数，中心只有一个
    const s2 = palindrome(s, i, i + 1) // 回文串长度为偶数，中心有两个
    res = res.length > s1.length ? res : s1
    res = res.length > s2.length ? res : s2
  }
  return res
}

function palindrome(s, l, r) {
  while (l >= 0 && r < s.length && s[l] === s[r]) {
    l--
    r++
  }
  return s.substring(l + 1, r)
}

20. 有效的括号

这道题我们可以用栈来解决，当我们遇到左括号（[、{、(）时，就把它们加入栈，当遇到配对的右括号的时候，把它们出栈。最后如果栈为空的话，说明括号就是有效的。

当然有些过程我们可以优化一下，比如用 map 保存左右括号方便查找，当我们遇到一个不配对的右括号的时候，直接返回 false。

/**
 * @param {string} s
 * @return {boolean}
 */
var isValid = function (s) {
  const map = {
    ')': '(',
    '}': '{',
    ']': '[',
  }
  const stack = []

  for (const char of s) {
    if (map[char]) {
      const c = stack.pop()
      if (c !== map[char]) return false
    } else {
      stack.push(char)
    }
  }
  return !stack.length
}

165. 比较版本号

分割 + 解析

版本号通过.分割，我们可以通过split将版本号分成一个一个的块，长度不足的可以在后面补0

之后比较每个块的数字就可以

/**
 * @param {string} version1
 * @param {string} version2
 * @return {number}
 */
var compareVersion = function (version1, version2) {
  const v1 = version1.split('.')
  const v2 = version2.split('.')
  let i = 0
  while (i < v1.length || i < v2.length) {
    const n1 = v1[i] ? parseInt(v1[i]) : 0
    const n2 = v2[i] ? parseInt(v2[i]) : 0
    if (n1 > n2) {
      return 1
    }
    if (n1 < n2) {
      return -1
    }
    i++
  }

  return 0
}

数组

1. 两数之和

哈希表

我们可以在遍历数组的时候使用map将nums[i]和下标i存下来，当遇到map中有值为target - nums[i]的键后就返回target - nums[i]的值和i组成的数组

var twoSum = function (nums, target) {
  const map = new Map()
  for (let i = 0; i < nums.length; i++) {
    if (map.has(target - nums[i])) {
      return [i, map.get(nums[i])]
    }
    map.set(nums[i], i)
  }
}

15. 三数之和

对于这道题，我门可以先固定一个数，从而转为两数之和问题，且这题需要的是元素而不是下标，所以可以采取排序+双指针的方式来接解题

主要的流程如下：

1. 遍历整个数组，每次固定一个数
2. 然后使用两个指针分别指向i+1和len-1，看这两个指针指向的数和之前固定的数的和是否为 0
   1. 如果为 0，那么就将这三个元素加入到ans，两个指着分别分别向左向右移动
   2. 如果小于 0，说明结果小了，那么就移动左指针
   3. 如果大于 0，说明结果打了，那么就移动右指针
3. 遍历完成后就可以返回ans数组

这里需要考虑到一个问题就是去重，我们不做处理的话，很有可能会有重复的组被加入结果。

因为数组是经过排序的，那么相等的数就会在一起，那么遇到一样的数的时候，后面直接跳过。

var threeSum = function (nums) {
  const len = nums.length
  const ans = []
  if (len < 3) return []
  nums.sort((a, b) => a - b)

  for (let i = 0; i < len; i++) {
    if (nums[i] > 0) break // 第一个数（最小的）大于 0 了，结果不可能为 0 了
    if (i > 0 && nums[i] === nums[i - 1]) continue // 去重
    let l = i + 1
    let r = len - 1
    while (l < r) {
      const sum = nums[i] + nums[l] + nums[r]
      if (sum < 0) {
        l++
      } else if (sum > 0) {
        r--
      } else {
        ans.push([nums[i], nums[l], nums[r]])
        while (l < r && nums[l] === nums[l + 1]) l++ // 去重
        while (l < r && nums[r] === nums[r - 1]) r-- // 去重
        l++
        r--
      }
    }
  }

  return ans
}

88. 合并两个有序数组

逆向双指针

因为nums1后面为空，可以直接覆盖，所以我们可以设置两个指针在两个数组最后（即nums1的指针在m-1，nums2的指针在n-1），从后向前遍历，将较大的元素放到 nums1 的最后面

var merge = function (nums1, m, nums2, n) {
  let p1 = m - 1,
    p2 = n - 1
  let tail = m + n - 1
  while (tail >= 0) {
    if (p1 < 0) {
      nums1[tail--] = nums2[p2--]
    } else if (p2 < 0) {
      nums1[tail--] = nums1[p1--]
    } else {
      nums1[tail--] = nums1[p1] >= nums2[p2] ? nums1[p1--] : nums2[p2--]
    }
  }
}

215. 数组中的第 K 个最大元素

我们要找到数组的第 K 大元素，首先想到要对数组进行排序，那有没有一种排序方法可以一遍排序，一遍让我们知道元素是第几大的元素呢？那就是快速排序

快速排序会确定一个pivot，排序一轮后，它左边的值都小于它，它右边的值都大于它，那么它的大小顺序就是它的下标。

这里需要注意：第 K 大元素的下标是nums.length - k，第一大元素是排序后的最后一个元素。

var findKthLargest = function (nums, k) {
  const target = nums.length - k // 转换一下，第 k 大元素的下标是 len - k
  let low = 0
  let high = nums.length - 1
  while (true) {
    const index = partition(nums, low, high)
    if (index === target) {
      return nums[target]
    } else if (index < target) {
      low = index + 1
    } else {
      high = index - 1
    }
  }
}

function partition(nums, low, high) {
  const mid = (low + high) >> 1
  swap(nums, low, mid)
  const start = low
  const pivot = nums[low]
  while (low < high) {
    while (low < high && nums[high] >= pivot) high--
    while (low < high && nums[low] <= pivot) low++
    swap(nums, low, high)
  }
  return hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.right, targetSum - root.val)
}

56. 合并区间

先排序

然后将最开始的区间加入res，之后的每个区间与res的最后一个区间的lastEnd值比较：

• 如果当前区间的curStart > lastEnd,，说明这两个区间不能合并，将该区间加入res
• 否则，说明两区间可以合并，选择lastEnd和curEnd中的最大值作为新的结尾（因为要考虑前一个区间完全包含当前区间的情况）

var merge = function (intervals) {
  intervals.sort((a, b) => a[0] - b[0])
  const res = [intervals[0]]

  for (let i = 0; i < intervals.length; i++) {
    const lastEnd = res[res.length - 1][1]
    const [curStart, curEnd] = intervals[i]

    if (curStart > lastEnd) {
      res.push(intervals[i])
    } else {
      res[res.length - 1][1] = Math.max(curEnd, lastEnd)
    }
  }

  return res
}

回溯

模板

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return

    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

46. 全排列

DFS

dfs函数有三个参数，分别是path保存遍历的路径，nums原数组，ans结果

回溯终止条件是 path 的长度和 nums 的长度相等，就可以将 path 加入 ans，需要注意的是需要用slice()获得 path 的深拷贝，避免获取的是 path 的引用

var permute = function (nums) {
  const res = []
  nums.forEach(n => dfs(res, nums, [n], [n]))
  return res
}

function dfs(res, nums, path) {
  if (path.length === nums.length) {
    res.push(path.slice())
    return
  }
  nums.forEach(n => {
    if (!path.includes(n)) {
      path.push(n)
      dfs(res, nums, path)
      path.pop()
    }
  })
}

22. 括号生成

var generateParenthesis = function (n) {
  const res = []

  dfs(res, n, [], 0)

  return res
}

function dfs(res, n, path, left) {
  if (path.length === n * 2) {
    res.push(path.join(''))
    return
  }

  if (left < n) {
    path.push('(')
    dfs(res, n, path.slice(), left + 1)
    path.pop()
  }

  if (path.length - left < left) {
    path.push(')')
    dfs(res, n, path.slice(), left)
    path.pop()
  }
}

动态规划

53. 最大子序和

动态规划

我们定义 dp[n] 为以 nums[n] 结尾的子数组最大和，我们可以想到 dp[n] 的最大值应该等于 dp[n - 1] 考虑加不加上 nums[n]，所以我们比较dp[n - 1] + nums[n]和nums[n] 的大小，其中较大的为 dp[n] 的值

那么有以下状态转移公式：

$$dp[n] = max{dp[n - 1] + nums[n],nums[n]}$$

初始值为 dp[0] = nums[0]

再用一个变量 max 记录一下 dp[n] 中的最大值

var maxSubArray = function (nums) {
  let max = nums[0]
  const dp = []
  dp[0] = nums[0]
  for (let i = 1; i < nums.length; i++) {
    dp[i] = Math.max(dp[i - 1] + nums[i], nums[i])
    max = Math.max(max, dp[i])
  }
  return max
}

300. 最长递增子序列

动态规划

1. 定义状态：

dp[i] 表示：以 nums[i] 结尾的最长上升子序列的长度

2. 状态转移方程：

如果一个较大的数接在较小的数后面，就会形成一个更长的子序列。只要 nums[i] 大于在它位置之前的某个数，那么 nums[i] 就可以接在这个数后面形成一个更长的上升子序列。所以我们找到符合nums[i] > nums[j]的dp[j]的最大值就可以了

$$dp[i] = \max_{0 \leq j<i,nums[j]<nums[i]}dp[j] + 1$$

3. 初始化：

dp[i] = 1，每个字符都可以认为是长度

var lengthOfLIS = function (nums) {
  const dp = new Array(nums.length).fill(1)
  let max = 1
  for (let i = 1; i < nums.length; i++) {
    for (let j = 0; j < i; j++) {
      if (nums[i] > nums[j]) {
        dp[i] = Math.max(dp[i], dp[j] + 1)
      }
    }
    max = Math.max(max, dp[i])
  }
  return max
}

322. 零钱兑换

状态定义：dp[i]表示组成金额i需要最少的硬币个数

base case：dp[0] = 0

状态转移：dp[i] = Math.min(dp[i - coin] + 1, dp[i])

当i - coin >= 0时，说明dp[i]可以由dp[i - coin]加coin这一个硬币组成

var coinChange = function (coins, amount) {
  const dp = new Array(amount + 1).fill(Infinity)

  dp[0] = 0
  for (let i = 0; i < dp.length; i++) {
    for (const coin of coins) {
      if (i - coin < 0) continue
      dp[i] = Math.min(dp[i - coin] + 1, dp[i])
    }
  }

  return dp[amount] === Infinity ? -1 : dp[amount]
}

718. 最长重复子数组

var findLength = function (nums1, nums2) {
  const m = nums1.length
  const n = nums2.length
  const dp = new Array(m + 1).fill(0).map(e => new Array(n + 1).fill(0))
  let max = 0
  for (let i = 1; i <= m; i++) {
    for (let j = 1; j <= n; j++) {
      // nums1[i-1] != nums2[j-1]的情况，初始化时已包括了
      if (nums1[i - 1] === nums2[j - 1]) {
        dp[i][j] = dp[i - 1][j - 1] + 1
      }
      max = Math.max(dp[i][j], max)
    }
  }

  return max
}

64. 最小路径和

var minPathSum = function (grid) {
  const m = grid.length
  const n = grid[0].length
  const dp = new Array(m).fill(0).map(() => new Array(n).fill(Infinity))
  dp[0][0] = grid[0][0]
  for (let i = 1; i < m; i++) {
    dp[i][0] = dp[i - 1][0] + grid[i][0]
  }

  for (let j = 1; j < n; j++) {
    dp[0][j] = dp[0][j - 1] + grid[0][j]
  }

  for (let i = 1; i < m; i++) {
    for (let j = 1; j < n; j++) {
      dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]
    }
  }

  return dp[m - 1][n - 1]
}

排序

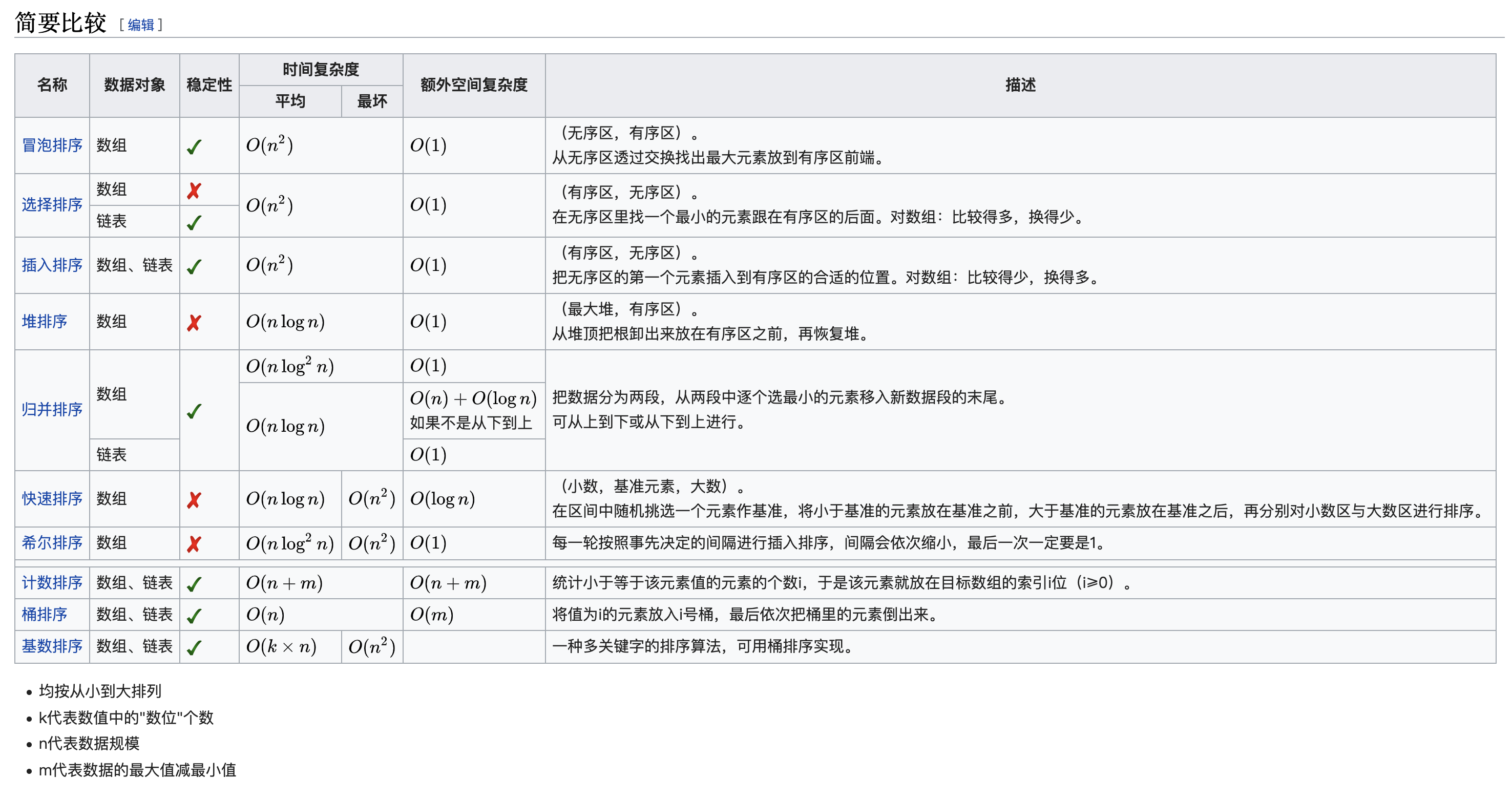
快速排序

var sortArray = function (nums) {
  quickSort(nums, 0, nums.length - 1)
  return nums
}

function quickSort(nums, low, high) {
  if (low >= high) return
  const pivot = partition(nums, low, high)
  quickSort(nums, low, pivot - 1)
  quickSort(nums, pivot + 1, high)
}

function partition(nums, low, high) {
  const mid = (low + high) >> 1
  swap(nums, mid, low)
  const pivot = nums[low]
  const start = low
  while (low < high) {
    while (low < high && nums[high] >= pivot) high--
    while (low < high && nums[low] <= pivot) low++
    swap(nums, low, high)
  }
  swap(nums, start, low)
  return low
}

function swap(nums, i, j) {
  ;[nums[i], nums[j]] = [nums[j], nums[i]]
}

贪心

121. 买卖股票的最佳时机

因为股票就买卖一次，那么贪心的想法很自然就是取最左最小值，取最右最大值，那么得到的差值就是最大利润。

var maxProfit = function (prices) {
  let low = Infinity
  let max = 0
  for (let i = 0; i < prices.length; i++) {
    low = Math.min(low, prices[i])
    max = Math.max(max, prices[i] - low)
  }
  return max
}

滑动窗口

框架

let left = 0, right = 0;

while (right < s.length) {
    // 增大窗口
    window.add(s[right]);
    right++;

    while (window needs shrink) {
        // 缩小窗口
        window.remove(s[left]);
        left++;
    }
}

3. 无重复字符的最长子串

双指针实现滑动窗口

遍历字符串，用 map 来存子串的字符，key 是 字符，value 是字符的个数，右指针每拿到一个字符 c ，就将 map[c] 的值加一，那么当 map[c] > 1 时，说明已经有字符重复，需要将左指针向右移动，左指针拿到的的字符 d，将 map[d] 的值减一，直到 map[c] == 1，即我们已经删除了重复的字符，这时候就可以记录最大长度。

需要注意的是，map 没有初始化，直接 map[c]++ 会有问题，我们需要判断一下 map[c] 为 undefined 的情况

map[c] = map[c] === undefined ? 1 : map[c] + 1

/**
 * @param {string} s
 * @return {number}
 */
var lengthOfLongestSubstring = function (s) {
  const map = {}
  let left = 0,
    right = 0
  let max = 0
  while (right < s.length) {
    const c = s[right]
    right++
    map[c] = map[c] === undefined ? 1 : map[c] + 1
    while (map[c] > 1) {
      const d = s[left]
      left++
      map[d]--
    }
    max = Math.max(max, right - left)
  }
  return max
}

209. 长度最小的子数组

我们确定好缩小窗口的条件是sum >= target，然后套用框架就行了

这里需要注意的是计算长度的时候是用r - l，因为这时候j已经是在下一个索引了不需加 1

var minSubArrayLen = function (target, nums) {
  const len = nums.length
  let l = (r = 0)
  let res = len + 1 // 子数组最大不会超过自身
  while (r < len) {
    // 窗口增大
    sum += nums[r++]
    // 窗口缩小
    while (sum >= target) {
      // r始终为开区间 [l, r)
      res = Math.min(res, r - l)
      sum -= nums[l++]
    }
  }
  return res > len ? 0 : res
}

栈

155. 最小栈

主要考点在常数时间内检索到最小元素，这就要求我们要将最小的元素保存下来

我们可以使用两个栈来实现，一个栈正常保存元素，另一个栈专门用来保存最小元素

关键在于push操作，我们需要判断保存最小元素的栈的入栈值：

如果最小栈为空时，那么入栈的就是val

如果最小栈不为空，需要判断val和最小栈栈顶元素的大小，入栈val和最小栈栈顶元素中小的元素

这样保证了两个栈元素数量相同，方便pop操作

class MinStack {
  constructor() {
    this.stack = []
    this.minStack = []
  }

  push(val) {
    this.stack.push(val)
    if (this.minStack.length === 0 || val <= this.minStack[this.minStack.length - 1]) {
      this.minStack.push(val)
    } else {
      this.minStack.push(this.minStack[this.minStack.length - 1])
    }
  }

  pop() {
    this.stack.pop()
    this.minStack.pop()
  }

  top() {
    return this.stack[this.stack.length - 1]
  }

  getMin() {
    return this.minStack[this.minStack.length - 1]
  }
}

146. LRU 缓存机制

哈希链表

唯一需要注意的是，put操作时，如果容量满了需要删除最不常用元素时，先删map中的key（因为需要this.dummyTail.prev.key拿到），然后再删链表中的this.dummyTail.prev节点

class LRUCache {
  constructor(capacity) {
    this.capacity = capacity
    this.map = new Map()
    this.dummyHead = new ListNode()
    this.dummyTail = new ListNode()
    this.dummyHead.next = this.dummyTail
    this.dummyTail.prev = this.dummyHead
  }

  get(key) {
    if (!this.map.has(key)) {
      return -1
    } else {
      const node = this.map.get(key)
      this.moveToHead(node)
      return node.value
    }
  }

  put(key, value) {
    if (this.map.has(key)) {
      const node = this.map.get(key)
      this.moveToHead(node)
      node.value = value
    } else {
      if (this.capacity === this.map.size) {
        this.map.delete(this.dummyTail.prev.key)
        this.removeNode(this.dummyTail.prev)
      }
      const node = new ListNode(key, value)
      this.addToHead(node)
      this.map.set(key, node)
    }
  }

  removeNode(node) {
    node.prev.next = node.next
    node.next.prev = node.prev
  }

  addToHead(node) {
    node.prev = this.dummyHead
    node.next = this.dummyHead.next
    this.dummyHead.next.prev = node
    this.dummyHead.next = node
  }

  moveToHead(node) {
    this.removeNode(node)
    this.addToHead(node)
  }
}

class ListNode {
  constructor(key, value) {
    this.key = key
    this.value = value
    this.next = null
    this.prev = null
  }
}

415. 字符串相加

双指针模拟

用指针模拟从后向前加，没有的位补零。

需要注意的是两个数取完了，但最后 carry 不为 0 时，需要多循环一次，因为这是 carry 在下一位

var addStrings = function (num1, num2) {
  let i = num1.length - 1,
    j = num2.length - 1
  let ans = []
  let carry = 0
  // 别忘了 carry
  while (i >= 0 || j >= 0 || carry) {
    const n1 = i >= 0 ? num1.charAt(i) - '0' : 0
    const n2 = j >= 0 ? num2.charAt(j) - '0' : 0
    const sum = n1 + n2 + carry
    carry = Math.floor(sum / 10)
    ans.push(sum % 10)
    i--
    j--
  }
  return ans.reverse().join('')
}

70. 爬楼梯

动态规划

因为我们一次可以爬 1 或 2 个台阶，那么爬到第 n+2 阶台阶的方法数就等于爬到第 n+1 阶台阶的方法数和爬到第 n 阶台阶的方法数之和

我们定义 dp[n] 为爬到第 n 阶台阶的方法数，我们可以推出状态转移公式：

$$dp[n+2] = dp[n+1] + dp[n+2]$$

初始状态为 dp[1] = 1，dp[2] = 2

var climbStairs = function (n) {
  const dp = []
  dp[1] = 1
  dp[2] = 2
  for (let i = 3; i <= n; i++) {
    dp[i] = dp[i - 1] + dp[i - 2]
  }
  return dp[n]
}

102. 二叉树的层序遍历

BFS

用一个数组保存每一层的节点，如果这个数组中没有元素，那么就终止遍历

var levelOrder = function (root) {
  if (root === null) return []
  const ans = []
  bfs([root], ans)
  return ans
}

const bfs = (list, ans) => {
  ans.push(list.map(e => e.val))
  const nextList = []
  list.forEach(e => {
    e.left !== null && nextList.push(e.left)
    e.right !== null && nextList.push(e.right)
  })
  if (!nextList.length) return
  bfs(nextList, ans)
}

94. 二叉树的中序遍历

方法一 递归

var inorderTraversal = function (root) {
  const res = []
  const inorder = root => {
    if (!root) {
      return
    }
    inorder(root.left)
    res.push(root.val)
    inorder(root.right)
  }
  inorder(root)
  return res
}

方法二 迭代

var inorderTraversal = function (root) {
  const res = []
  const stk = []
  while (root || stk.length) {
    while (root) {
      stk.push(root)
      root = root.left
    }
    root = stk.pop()
    res.push(root.val)
    root = root.right
  }
  return res
}

剑指 Offer 10- I. 斐波那契数列

动态规划

状态定义：dp[i]表示斐波那契数列第 i 项的值

状态转移方程：dp[i] = (dp[i - 1] + dp[i - 2]) % 1000000007 （本题要求取模）

初始状态：dp = [0,1]

输出：dp[n]

const fib = n => {
  const dp = [0, 1]
  for (let i = 2; i <= n; i++) {
    dp[i] = (dp[i - 1] + dp[i - 2]) % 1000000007
  }
  return dp[n]
}

322. 零钱兑换

动态规划

状态定义：dp[i]表示凑齐 i 元所需最少的硬币个数

状态转移方程：dp[i] = min(dp[i],dp[i - coin] + 1) ，其中 coin 为 coins 中的每个元素

初始状态：dp[0] = 0

输出：如果没有能组成总金额的话输出 -1，否则输出dp[amount]

var coinChange = function (coins, amount) {
  const dp = new Array(amount + 1).fill(Infinity)
  dp[0] = 0
  for (let i = 1; i <= amount; i++) {
    for (let coin of coins) {
      if (coin <= i) {
        dp[i] = Math.min(dp[i], dp[i - coin] + 1)
      }
    }
  }
  return dp[amount] === Infinity ? -1 : dp[amount]
}

56. 合并区间

先排序，后看区间

我们首先将intervals数组根据start升序排序来保证每个区间是连续的，接着用ans数组来保存结果。

首先将排序后的数组sorted的第一个区间放入ans中，之后的sorted每个区间与ans的最后一个区间比较：

• 如果当前区间的curEnd小于lastEnd，说明区间不重合，直接将当前区间加入ans
• 否则区间重合，将ans的最后一个区间的end更新为curEnd和lastEnd之中较大的值

var merge = function (intervals) {
  let ans = []
  let sorted = intervals.sort((left, right) => left[0] - right[0])
  ans.push(sorted[0])
  for (let i = 1; i < sorted.length; i++) {
    const [_, lastEnd] = ans[ans.length - 1]
    const [curStart, curEnd] = sorted[i]
    if (curStart > lastEnd) {
      ans.push(sorted[i])
    } else {
      ans[ans.length - 1][1] = Math.max(lastEnd, curEnd)
    }
  }
  return ans
}

200. 岛屿数量

网格题的 DFS 基本框架

对于这种网格的题我们可以将它想成是一个四叉树，即上、下、左、右，四个方向

遍历过程中会出现一些越界的问题，我们利用“先污染后治理”的思想来统一遍历过程，即可以超出边界，下一轮遍历再判断是否超出边界

对于二叉树来说就是节点是否为 null，而对于网格来说就是是否超出网格范围，若超出则直接返回

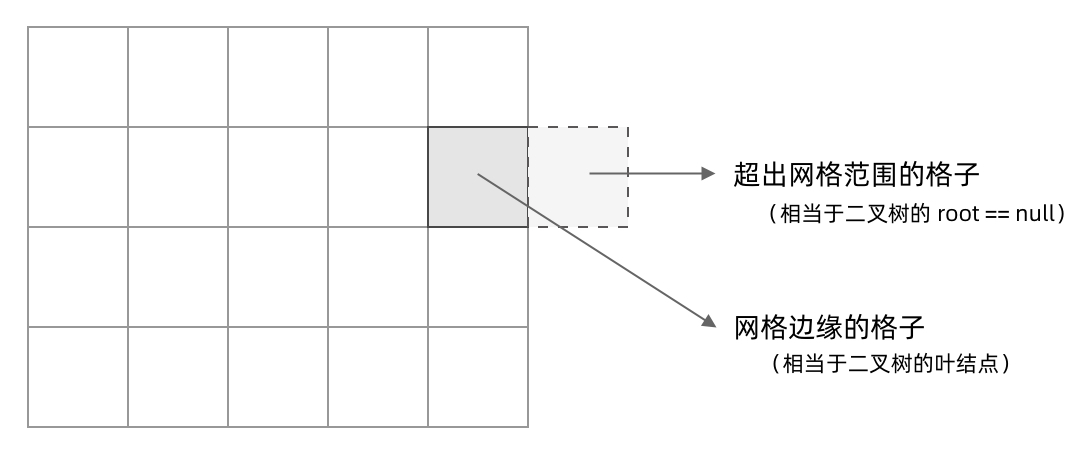
于是，我们可以建立这么一个框架

function dfs(grid, i, j) {
  // 如果越界直接返回
  if (!inArea(grid, i, j)) {
    return
  }

  // 访问上下左右
  dfs(grid, i + 1, j)
  dfs(grid, i - 1, j)
  dfs(grid, i, j + 1)
  dfs(grid, i, j - 1)
}

接下来，我们还需要避免一个问题，那就是之前遍历过的点，之后就不需要遍历了，防止死循环出现，如图：

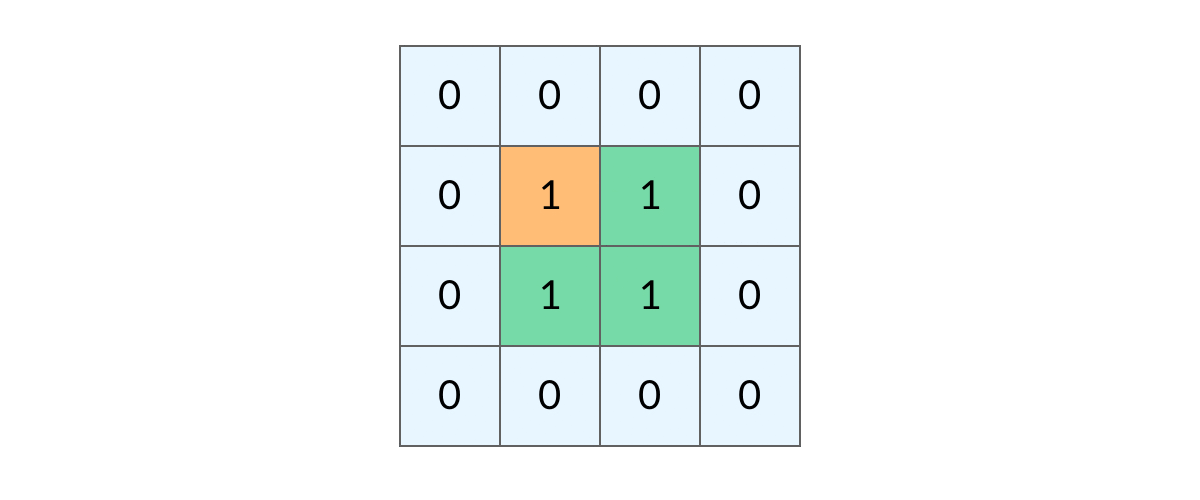
所以我们需要标记一下已经遍历过的格子

function dfs(grid, i, j) {
  // 如果越界或不是未遍历过的陆地直接返回
  if (!inArea(grid, i, j) || grid[i][j] != '1') {
    return
  }

  // 标记陆地为已遍历
  grid[i][j] = '2'

  // 访问上下左右
  dfs(grid, i + 1, j)
  dfs(grid, i - 1, j)
  dfs(grid, i, j + 1)
  dfs(grid, i, j - 1)
}

对于本题，代码如下：

var numIslands = function (grid) {
  let count = 0

  for (let i = 0; i < grid.length; i++) {
    for (let j = 0; j < grid[0].length; j++) {
      if (grid[i][j] == '1') {
        dfs(grid, i, j)
        ++count
      }
    }
  }

  return count
}

function dfs(grid, i, j) {
  if (!inArea(grid, i, j) || grid[i][j] != '1') {
    return
  }

  grid[i][j] = '2'

  dfs(grid, i + 1, j)
  dfs(grid, i - 1, j)
  dfs(grid, i, j + 1)
  dfs(grid, i, j - 1)
}

function inArea(grid, i, j) {
  return i >= 0 && i < grid.length && j >= 0 && j < grid[0].length
}

236. 二叉树的最近公共祖先

祖先：若节点 p 在节点 root 的左（右）子树中，或 p = root，则称 root 是 p 的祖先

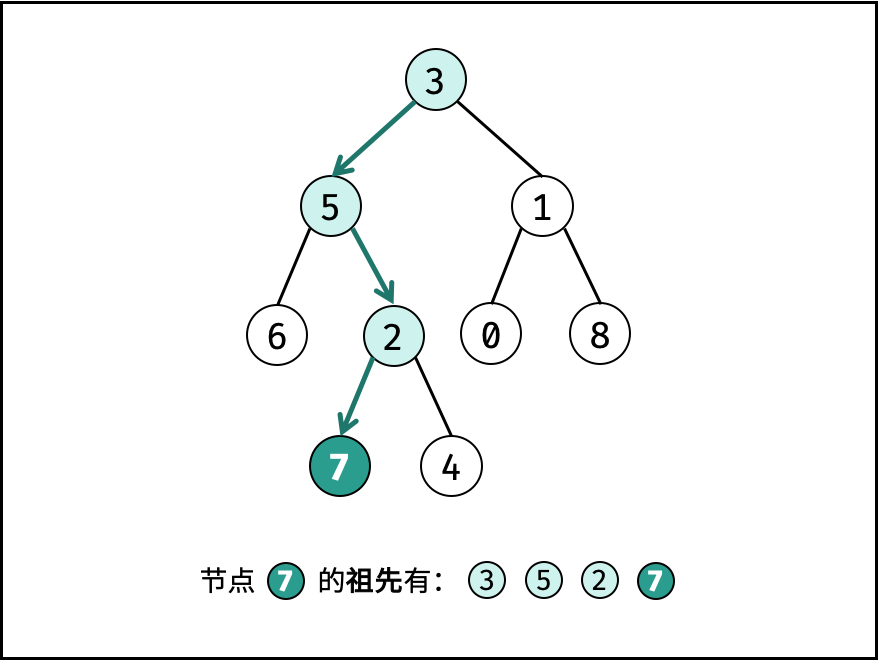
根据定义，若 root 是 p，q 的最近公共祖先，只有三种情况：

1. p 和 q 在 root 的子树中，且分别在左、右子树中
2. p = root，且 q 在 root 的子树中
3. q = root ，且 p 在 root 的子树中

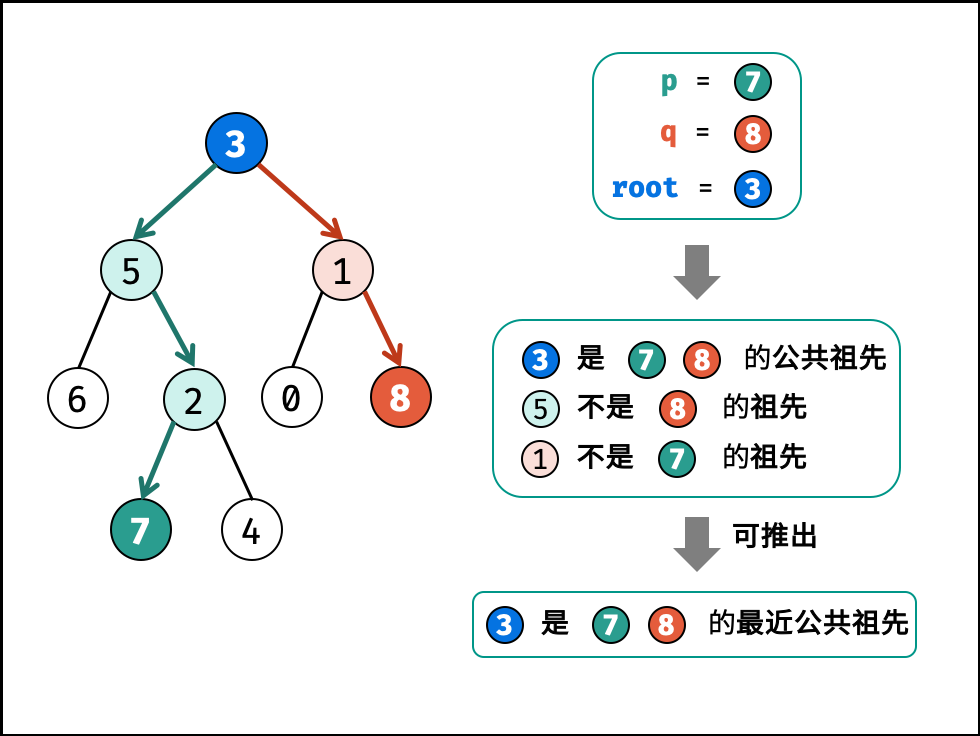
下面就来分析一下递归函数lowestCommonAncestor:

1. 终止条件：

   • root == null时，返回 null 这是二叉树递归的常规终止条件
   • root === p || root === q，root 本身就是 p 或 q，也就是找到了要找的节点，那么就返回 root

2. 递归状态：

   分别递归左、右子树，左子树返回值为left，右子树返回值为right

3. 函数返回值：

   • 当left和right都不为空时，那么它们一定是 p 和 q，root 就为它们的最近公共祖先（这里因为我们用的是二叉树的后序遍历，就好比从p和q出发往上走，第一次相交的节点就是这个root，即最近公共祖先）
   • 当left和right都为空时，返回null
   • 当left和right有一个不为空，那么就返回不为空的节点，即是返回了 p 或者 q，或是它们的最近公共祖先

var lowestCommonAncestor = function (root, p, q) {
  if (root == null) return

  if (root === p || root === q) return root

  const left = lowestCommonAncestor(root.left, p, q)
  const right = lowestCommonAncestor(root.right, p, q)

  if (left && right) return root

  if (!left && !right) return null

  return left == null ? right : left
}